Path and CrossSection

You can create a Path in gdsfactory and extrude it with an arbitrary CrossSection.

Lets create a path:

Create a blank Path.
Append points to the Path either using the built-in functions (arc(), straight(), euler() ...) or by providing your own lists of points
Specify CrossSection with layers and offsets.
Extrude Path with a CrossSection to create a Component with the path polygons in it.

import matplotlib.pyplot as plt
import numpy as np

import gdsfactory as gf

Path¶

The first step is to generate the list of points we want the path to follow. Let’s start out by creating a blank Path and using the built-in functions to make a few smooth turns.

p1 = gf.path.straight(length=5)
p2 = gf.path.euler(radius=5, angle=45, p=0.5, use_eff=False)
p = p1 + p2
f = p.plot()

p1 = gf.path.straight(length=5)
p2 = gf.path.euler(radius=5, angle=45, p=0.5, use_eff=False)
p = p2 + p1
f = p.plot()

P = gf.Path()
P += gf.path.arc(radius=10, angle=90)  # Circular arc
P += gf.path.straight(length=10)  # Straight section
P += gf.path.euler(radius=3, angle=-90)  # Euler bend (aka "racetrack" curve)
P += gf.path.straight(length=40)
P += gf.path.arc(radius=8, angle=-45)
P += gf.path.straight(length=10)
P += gf.path.arc(radius=8, angle=45)
P += gf.path.straight(length=10)

f = P.plot()

p2 = P.copy().rotate(45)
f = p2.plot()

P.points - p2.points

array([[  0.        ,   0.        ],
       [  0.07775818,  -0.18109421],
       [  0.16015338,  -0.36012627],
       [  0.24713097,  -0.53697746],
       [  0.33863327,  -0.71153054],
       [  0.43459961,  -0.88366975],
       [  0.53496636,  -1.05328096],
       [  0.63966697,  -1.2202517 ],
       [  0.74863202,  -1.38447127],
       [  0.86178925,  -1.54583076],
       [  0.97906364,  -1.7042232 ],
       [  1.10037742,  -1.85954356],
       [  1.22565016,  -2.01168884],
       [  1.35479879,  -2.16055818],
       [  1.48773767,  -2.30605285],
       [  1.62437867,  -2.44807638],
       [  1.76463118,  -2.58653461],
       [  1.9084022 ,  -2.72133573],
       [  2.0555964 ,  -2.85239035],
       [  2.20611618,  -2.97961158],
       [  2.35986175,  -3.10291506],
       [  2.51673115,  -3.22221903],
       [  2.67662037,  -3.33744439],
       [  2.83942339,  -3.44851474],
       [  3.00503227,  -3.55535642],
       [  3.1733372 ,  -3.6578986 ],
       [  3.34422657,  -3.75607328],
       [  3.51758709,  -3.84981537],
       [  3.69330379,  -3.93906271],
       [  3.87126017,  -4.02375613],
       [  4.05133823,  -4.10383946],
       [  4.23341856,  -4.1792596 ],
       [  4.41738044,  -4.24996655],
       [  4.60310189,  -4.31591343],
       [  4.79045976,  -4.3770565 ],
       [  4.97932982,  -4.43335522],
       [  5.16958684,  -4.48477228],
       [  5.36110467,  -4.53127356],
       [  5.55375631,  -4.57282824],
       [  5.74741403,  -4.60940877],
       [  5.94194941,  -4.64099089],
       [  6.13723348,  -4.66755366],
       [  6.33313674,  -4.68907946],
       [  6.52952929,  -4.70555403],
       [  6.72628092,  -4.71696644],
       [  6.92326117,  -4.72330911],
       [  7.12033942,  -4.72457786],
       [  7.317385  ,  -4.72077183],
       [  7.51426725,  -4.71189355],
       [  7.71085564,  -4.69794891],
       [  7.90701981,  -4.67894715],
       [  8.10262968,  -4.65490087],
       [  8.29755556,  -4.62582602],
       [  8.4916682 ,  -4.59174187],
       [  8.6848389 ,  -4.55267103],
       [  8.87693955,  -4.50863939],
       [  9.0678428 ,  -4.45967617],
       [  9.25742205,  -4.40581381],
       [  9.44555161,  -4.34708805],
       [  9.63210673,  -4.28353781],
       [  9.81696372,  -4.21520523],
       [ 10.        ,  -4.14213562],
       [ 17.07106781,  -1.21320344],
       [ 17.22259744,  -1.15062977],
       [ 17.3745295 ,  -1.0890412 ],
       [ 17.52724719,  -1.02943054],
       [ 17.68109502,  -0.9728054 ],
       [ 17.83635884,  -0.92019408],
       [ 17.99324531,  -0.87264941],
       [ 18.15186066,  -0.83125013],
       [ 18.31218874,  -0.79709882],
       [ 18.47406876,  -0.77131591],
       [ 18.63717281,  -0.75502883],
       [ 18.80098407,  -0.74935572],
       [ 18.98113405,  -0.75643383],
       [ 19.16017334,  -0.77762453],
       [ 19.33699811,  -0.81279716],
       [ 19.51051817,  -0.86173488],
       [ 19.67966373,  -0.92413597],
       [ 19.84339193,  -0.9996157 ],
       [ 20.00069333,  -1.08770872],
       [ 20.15059814,  -1.18787191],
       [ 20.29218212,  -1.29948772],
       [ 20.42457237,  -1.42186801],
       [ 20.53639293,  -1.54171156],
       [ 20.6402082 ,  -1.66856024],
       [ 20.73644339,  -1.80125797],
       [ 20.82566384,  -1.93877567],
       [ 20.90854811,  -2.08020737],
       [ 20.98586445,  -2.22476202],
       [ 21.05845073,  -2.37175194],
       [ 21.12719755,  -2.5205788 ],
       [ 21.19303416,  -2.67071762],
       [ 21.25691665,  -2.82169951],
       [ 21.31981802,  -2.97309339],
       [ 33.03554677, -31.25736464],
       [ 33.1091836 , -31.44370627],
       [ 33.17668408, -31.63235747],
       [ 33.23797592, -31.82311621],
       [ 33.29299349, -32.01577822],
       [ 33.34167789, -32.21013721],
       [ 33.38397696, -32.40598505],
       [ 33.41984543, -32.60311201],
       [ 33.44924488, -32.80130701],
       [ 33.47214384, -33.00035782],
       [ 33.48851777, -33.20005129],
       [ 33.49834914, -33.40017358],
       [ 33.50162744, -33.60051039],
       [ 33.49834914, -33.80084721],
       [ 33.48851777, -34.0009695 ],
       [ 33.47214384, -34.20066296],
       [ 33.44924488, -34.39971377],
       [ 33.41984543, -34.59790877],
       [ 33.38397696, -34.79503574],
       [ 33.34167789, -34.99088357],
       [ 33.29299349, -35.18524256],
       [ 33.23797592, -35.37790458],
       [ 33.17668408, -35.56866332],
       [ 33.1091836 , -35.75731451],
       [ 33.03554677, -35.94365614],
       [ 30.10661458, -43.01472396],
       [ 30.03297776, -43.20106559],
       [ 29.96547728, -43.38971678],
       [ 29.90418544, -43.58047552],
       [ 29.84916786, -43.77313754],
       [ 29.80048347, -43.96749653],
       [ 29.75818439, -44.16334436],
       [ 29.72231592, -44.36047132],
       [ 29.69291647, -44.55866633],
       [ 29.67001752, -44.75771713],
       [ 29.65364359, -44.9574106 ],
       [ 29.64381221, -45.15753289],
       [ 29.64053392, -45.35786971],
       [ 29.64381221, -45.55820652],
       [ 29.65364359, -45.75832881],
       [ 29.67001752, -45.95802228],
       [ 29.69291647, -46.15707309],
       [ 29.72231592, -46.35526809],
       [ 29.75818439, -46.55239505],
       [ 29.80048347, -46.74824289],
       [ 29.84916786, -46.94260187],
       [ 29.90418544, -47.13526389],
       [ 29.96547728, -47.32602263],
       [ 30.03297776, -47.51467382],
       [ 30.10661458, -47.70101546],
       [ 33.03554677, -54.77208327]])

You can also modify our Path in the same ways as any other gdsfactory object:

Manipulation with move(), rotate(), mirror(), etc
Accessing properties like xmin, y, center, bbox, etc

P.movey(10)
P.xmin = 20
f = P.plot()

You can also check the length of the curve with the length() method:

P.length()

105.341

CrossSection¶

Now that you’ve got your path defined, the next step is to define the cross-section of the path. To do this, you can create a blank CrossSection and add whatever cross-sections you want to it. You can then combine the Path and the CrossSection using the gf.path.extrude() function to generate a Component:

Option 1: Single layer and width cross-section¶

The simplest option is to just set the cross-section to be a constant width by passing a number to extrude() like so:

# Extrude the Path and the CrossSection
c = gf.path.extrude(P, layer=(1, 0), width=1.5)
c.plot()

Option 2: Arbitrary Cross-section¶

You can also extrude an arbitrary cross_section

Now, what if we want a more complicated straight? For instance, in some photonic applications it’s helpful to have a shallow etch that appears on either side of the straight (often called a trench or sleeve). Additionally, it might be nice to have a Port on either end of the center section so we can snap other geometries to it. Let’s try adding something like that in:

p = gf.path.straight()

# Add a few "sections" to the cross-section
s0 = gf.Section(width=1, offset=0, layer=(1, 0), port_names=("in", "out"))
s1 = gf.Section(width=2, offset=2, layer=(2, 0))
s2 = gf.Section(width=2, offset=-2, layer=(2, 0))
x = gf.CrossSection(sections=(s0, s1, s2))

c = gf.path.extrude(p, cross_section=x)
c.plot()

p = gf.path.arc()

# Combine the Path and the CrossSection
b = gf.path.extrude(p, cross_section=x)
b.plot()

Option 3: CrossSection with ComponentAlongPath¶

You can also place components along a path, which is useful for wiring vias.

import gdsfactory as gf
from gdsfactory.cross_section import ComponentAlongPath

# Create the path
p = gf.path.straight()
p += gf.path.arc(10)
p += gf.path.straight()

# Define a cross-section with a via
via = ComponentAlongPath(
    component=gf.c.rectangle(size=(1, 1), centered=True), spacing=5, padding=2
)
s = gf.Section(width=0.5, offset=0, layer=(1, 0), port_names=("in", "out"))
x = gf.CrossSection(sections=(s,), components_along_path=(via,))

# Combine the path with the cross-section
c = gf.path.extrude(p, cross_section=x)
c.plot()

import gdsfactory as gf
from gdsfactory.cross_section import ComponentAlongPath

# Create the path
p = gf.path.straight()
p += gf.path.arc(10)
p += gf.path.straight()

# Define a cross-section with a via
via0 = ComponentAlongPath(component=gf.c.via1(), spacing=5, padding=2, offset=0)
viap = ComponentAlongPath(component=gf.c.via1(), spacing=5, padding=2, offset=+2)
vian = ComponentAlongPath(component=gf.c.via1(), spacing=5, padding=2, offset=-2)
x = gf.CrossSection(sections=[s], components_along_path=(via0, viap, vian))

# Combine the path with the cross-section
c = gf.path.extrude(p, cross_section=x)
c.plot()

Path¶

You can pass append() lists of path segments. This makes it easy to combine paths very quickly. Below we show 3 examples using this functionality:

Example 1: Assemble a complex path by making a list of Paths and passing it to append()

import gdsfactory as gf

P = gf.Path()

# Create the basic Path components
left_turn = gf.path.euler(radius=4, angle=90)
right_turn = gf.path.euler(radius=4, angle=-90)
straight = gf.path.straight(length=10)

# Assemble a complex path by making list of Paths and passing it to `append()`
P.append(
    [
        straight,
        left_turn,
        straight,
        right_turn,
        straight,
        straight,
        right_turn,
        left_turn,
        straight,
    ]
)

f = P.plot()

P = (
    straight
    + left_turn
    + straight
    + right_turn
    + straight
    + straight
    + right_turn
    + left_turn
    + straight
)
f = P.plot()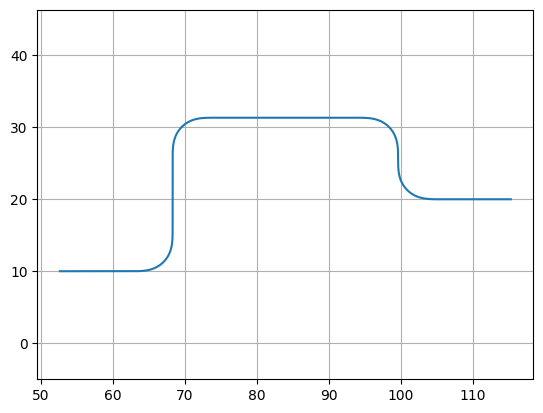

Example 2: Create an “S-turn” just by making a list of [left_turn, right_turn]

P = gf.Path()

# Create an "S-turn" just by making a list
s_turn = [left_turn, right_turn]

P.append(s_turn)
f = P.plot()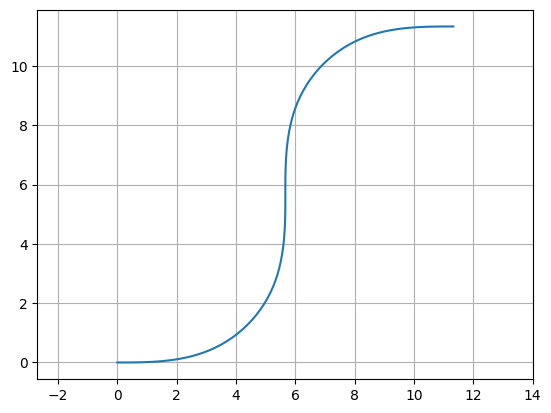

Example 3: Repeat the S-turn 3 times by nesting our S-turn list in another list

P = gf.Path()

# Create an "S-turn" using a list
s_turn = [left_turn, right_turn]

# Repeat the S-turn 3 times by nesting our S-turn list 3x times in another list
triple_s_turn = [s_turn, s_turn, s_turn]

P.append(triple_s_turn)
f = P.plot()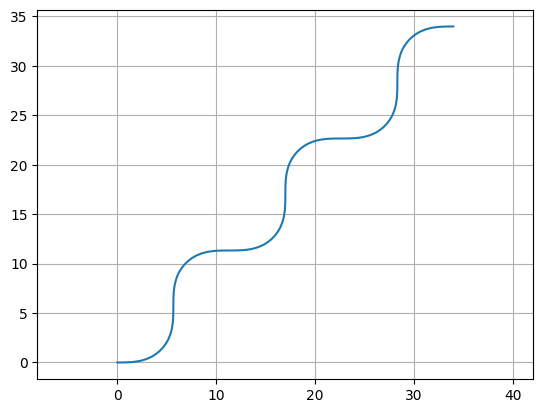

Note you can also use the Path() constructor to immediately construct your Path:

P = gf.Path([straight, left_turn, straight, right_turn, straight])
f = P.plot()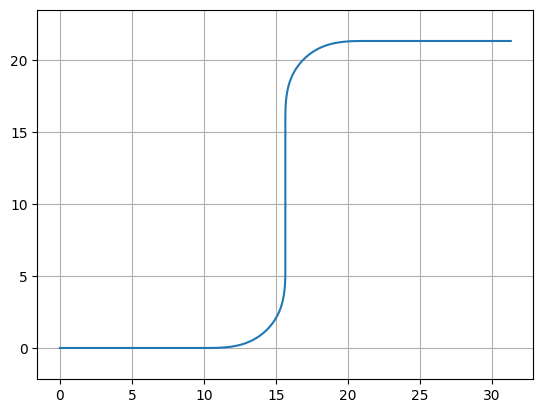

Waypoint smooth paths¶

You can also build smooth paths between waypoints with the smooth() function

points = np.array([(20, 10), (40, 10), (20, 40), (50, 40), (50, 20), (70, 20)])
plt.plot(points[:, 0], points[:, 1], ".-")
plt.axis("equal")

(np.float64(17.5), np.float64(72.5), np.float64(8.5), np.float64(41.5))

points = np.array([(20, 10), (40, 10), (20, 40), (50, 40), (50, 20), (70, 20)])

P = gf.path.smooth(
    points=points,
    radius=2,
    bend=gf.path.euler,  # Alternatively, use pp.arc
    use_eff=False,
)
f = P.plot()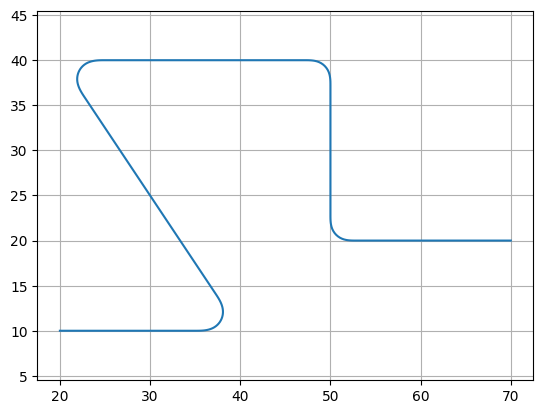

Waypoint sharp paths¶

It’s also possible to make more traditional angular paths (e.g. electrical wires) in a few different ways.

Example 1: Using a simple list of points

P = gf.Path([(20, 10), (30, 10), (40, 30), (50, 30), (50, 20), (70, 20)])
f = P.plot()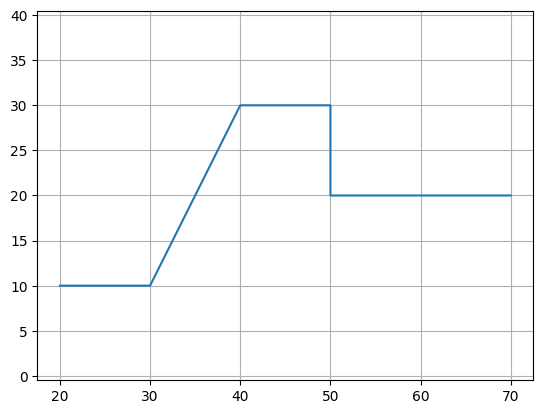

Example 2: Using the “turn and move” method, where you manipulate the end angle of the Path so that when you append points to it, they’re in the correct direction. Note: It is crucial that the number of points per straight section is set to 2 (gf.path.straight(length, num_pts = 2)) otherwise the extrusion algorithm will show defects.

P = gf.Path()
P += gf.path.straight(length=10, npoints=2)
P.end_angle += 90  # "Turn" 90 deg (left)
P += gf.path.straight(length=10, npoints=2)  # "Walk" length of 10
P.end_angle += -135  # "Turn" -135 degrees (right)
P += gf.path.straight(length=15, npoints=2)  # "Walk" length of 10
P.end_angle = 0  # Force the direction to be 0 degrees
P += gf.path.straight(length=10, npoints=2)  # "Walk" length of 10
f = P.plot()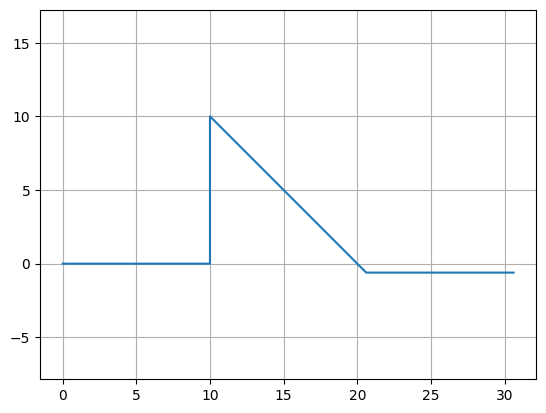

s0 = gf.Section(width=1, offset=0, layer=(1, 0))
s1 = gf.Section(width=1.5, offset=2.5, layer=(2, 0))
s2 = gf.Section(width=1.5, offset=-2.5, layer=(3, 0))
X = gf.CrossSection(sections=[s0, s1, s2])
c = gf.path.extrude(P, X)
c.plot()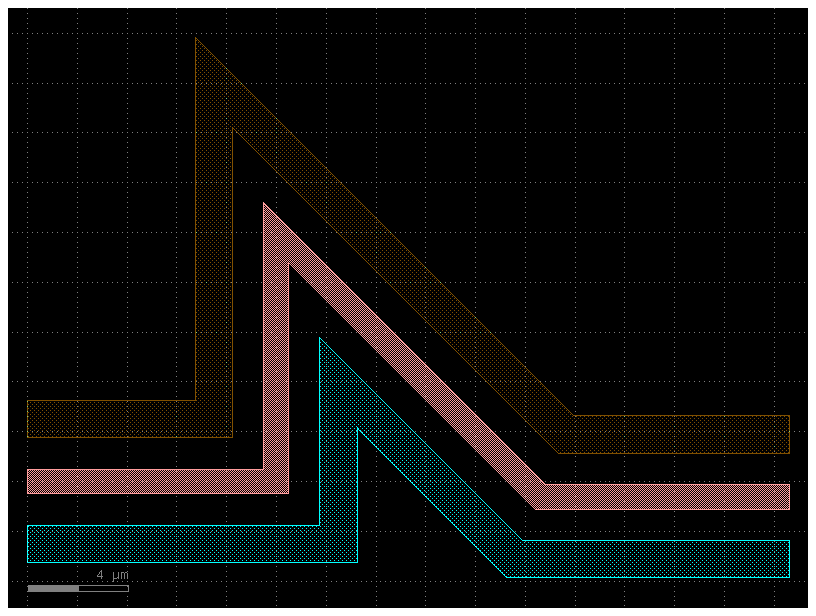

Custom curves¶

Now let’s have some fun and try to make a loop-de-loop structure with parallel straights and several Ports.

To create a new type of curve we simply make a function that produces an array of points. The best way to do that is to create a function which allows you to specify a large number of points along that curve -- in the case below, the looploop() function outputs 1000 points along a looping path. Later, if we want reduce the number of points in our geometry we can trivially simplify the path.

def looploop(num_pts=1000):
    """Simple limacon looping curve."""
    t = np.linspace(-np.pi, 0, num_pts)
    r = 20 + 25 * np.sin(t)
    x = r * np.cos(t)
    y = r * np.sin(t)
    return np.array((x, y)).T


# Create the path points
P = gf.Path()
P.append(gf.path.arc(radius=10, angle=90))
P.append(gf.path.straight())
P.append(gf.path.arc(radius=5, angle=-90))
P.append(looploop(num_pts=1000))
P.rotate(-45)

# Create the crosssection
s0 = gf.Section(width=1, offset=0, layer=(1, 0), port_names=("in", "out"))
s1 = gf.Section(width=0.5, offset=2, layer=(2, 0))
s2 = gf.Section(width=0.5, offset=4, layer=(3, 0))
s3 = gf.Section(width=1, offset=0, layer=(4, 0))
X = gf.CrossSection(sections=(s0, s1, s2, s3))

c = gf.path.extrude(P, X)
c.plot()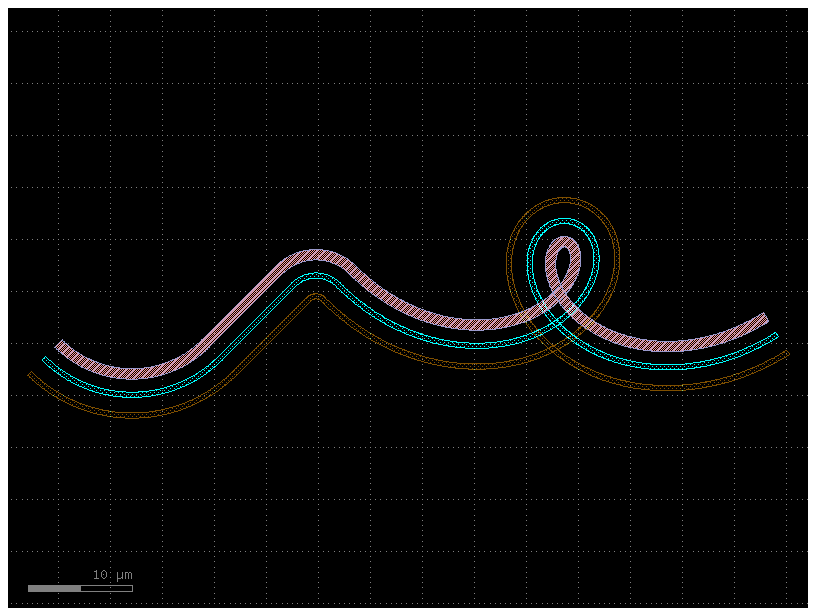

You can create Paths from any array of points -- just be sure that they form smooth curves! If we examine our path P we can see that all we’ve simply created a long list of points:

path_points = P.points  # Curve points are stored as a numpy array in P.points
print(np.shape(path_points))  # The shape of the array is Nx2
print(len(P))  # Equivalently, use len(P) to see how many points are inside

(1092, 2)
1092

Simplifying / reducing point usage¶

One of the chief concerns of generating smooth curves is that too many points are generated, inflating file sizes and making boolean operations computationally expensive. Fortunately, PHIDL has a fast implementation of the Ramer-Douglas–Peucker algorithm that lets you reduce the number of points in a curve without changing its shape. All that needs to be done is when you made a component component() extruding the path with a cross_section, you specify the simplify argument.

If we specify simplify = 1e-3, the number of points in the line drops from 12,000 to 4,000, and the remaining points form a line that is identical to within 1e-3 distance from the original (for the default 1 micron unit size, this corresponds to 1 nanometer resolution):

# The remaining points form a identical line to within `1e-3` from the original
c = gf.path.extrude(p=P, cross_section=X, simplify=1e-3)
c.plot()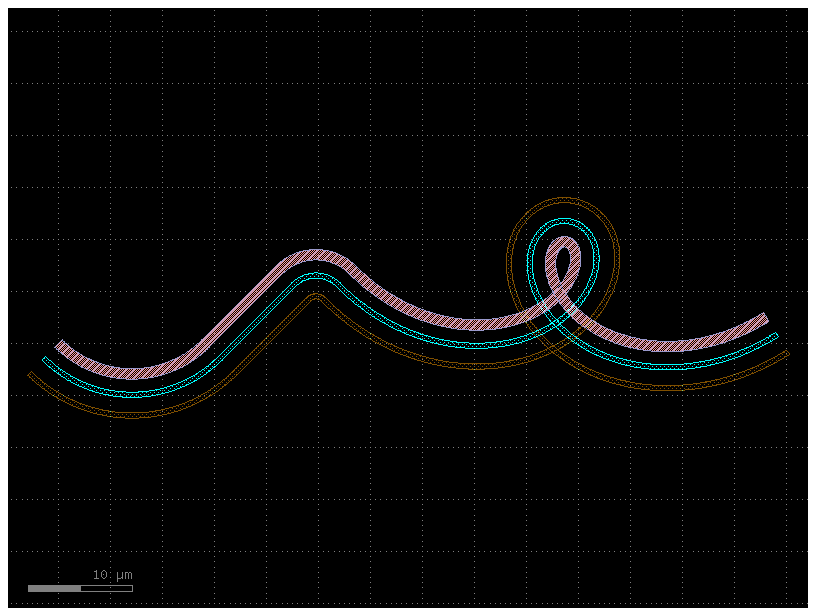

Let’s say we need fewer points. We can increase the simplify tolerance by specifying simplify = 1e-1. This drops the number of points to ~400 points form a line that is identical to within 1e-1 distance from the original:

c = gf.path.extrude(P, cross_section=X, simplify=1e-1)
c.plot()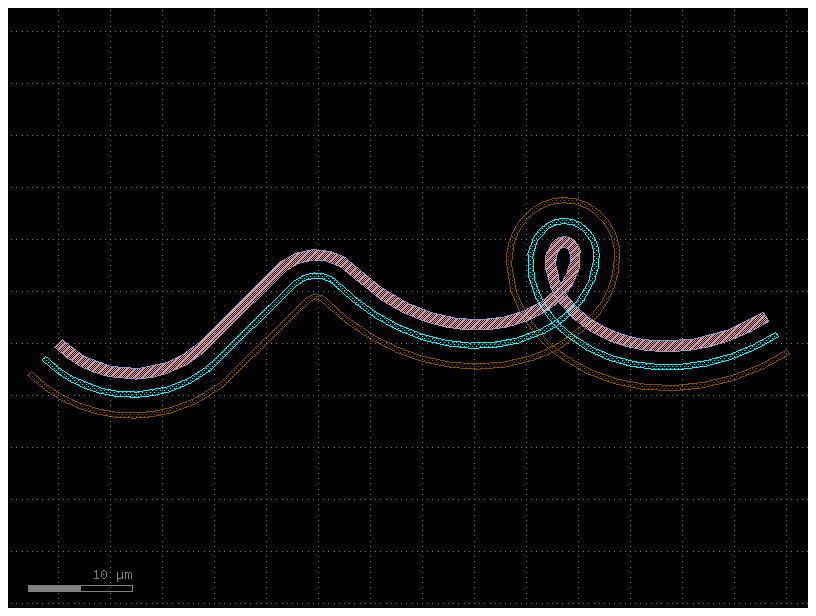

Taken to absurdity, what happens if we set simplify = 0.3? Once again, the ~200 remaining points form a line that is within 0.3 units from the original -- but that line looks pretty bad.

c = gf.path.extrude(P, cross_section=X, simplify=0.3)
c.plot()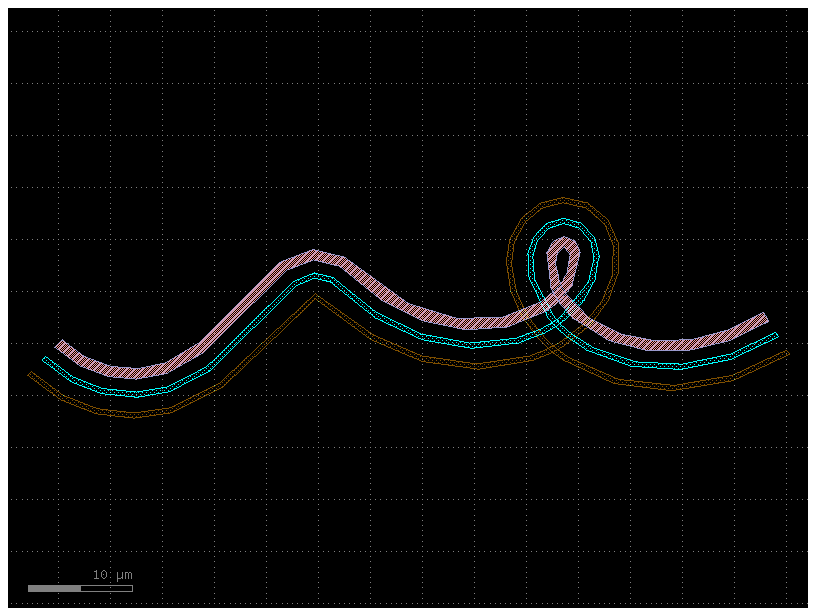

Curvature calculation¶

The Path class has a curvature() method that computes the curvature K of your smooth path (K = 1/(radius of curvature)). This can be helpful for verifying that your curves transition smoothly such as in track-transition curves (also known as “Euler” bends in the photonics world). Euler bends have lower mode-mismatch loss as explained in this paper

Note this curvature is numerically computed so areas where the curvature jumps instantaneously (such as between an arc and a straight segment) will be slightly interpolated, and sudden changes in point density along the curve can cause discontinuities.

straight_points = 100

P = gf.Path()
P.append(
    [
        gf.path.straight(
            length=10, npoints=straight_points
        ),  # Should have a curvature of 0
        gf.path.euler(
            radius=3, angle=90, p=0.5, use_eff=False
        ),  # Euler straight-to-bend transition with min. bend radius of 3 (max curvature of 1/3)
        gf.path.straight(
            length=10, npoints=straight_points
        ),  # Should have a curvature of 0
        gf.path.arc(radius=10, angle=90),  # Should have a curvature of 1/10
        gf.path.arc(radius=5, angle=-90),  # Should have a curvature of -1/5
        gf.path.straight(
            length=2, npoints=straight_points
        ),  # Should have a curvature of 0
    ]
)

f = P.plot()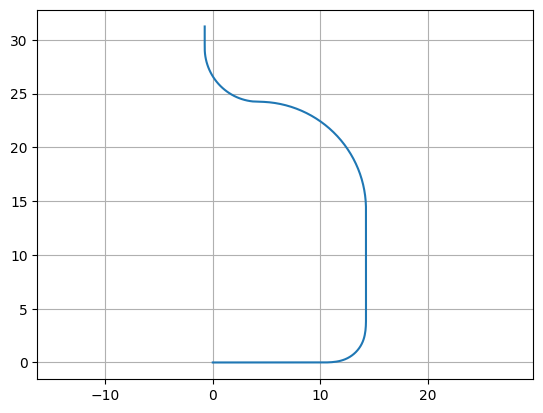

Arc paths are equivalent to bend_circular and euler paths are equivalent to bend_euler

s, K = P.curvature()
plt.plot(s, K, ".-")
plt.xlabel("Position along curve (arc length)")
plt.ylabel("Curvature")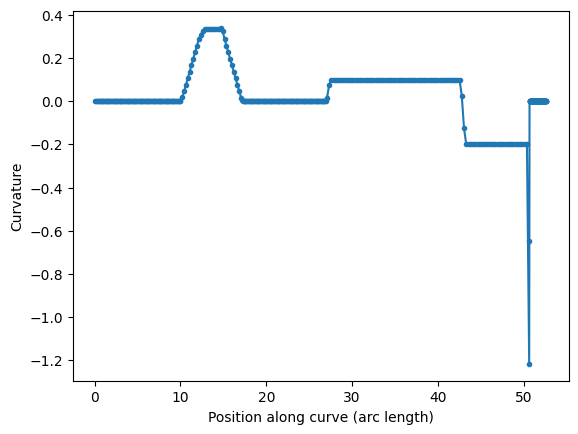

P = gf.path.euler(radius=3, angle=90, p=1.0, use_eff=False)
P.append(gf.path.euler(radius=3, angle=90, p=0.2, use_eff=False))
P.append(gf.path.euler(radius=3, angle=90, p=0.0, use_eff=False))
P.plot()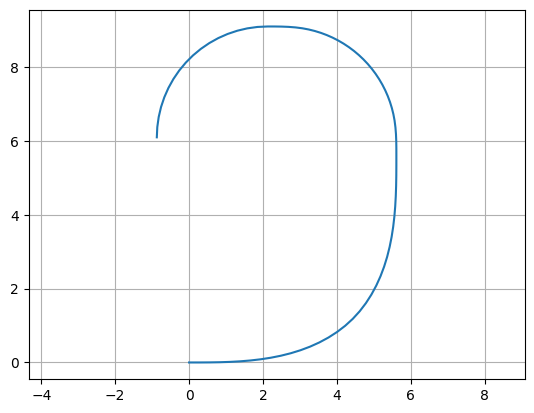

s, K = P.curvature()
plt.plot(s, K, ".-")
plt.xlabel("Position along curve (arc length)")
plt.ylabel("Curvature")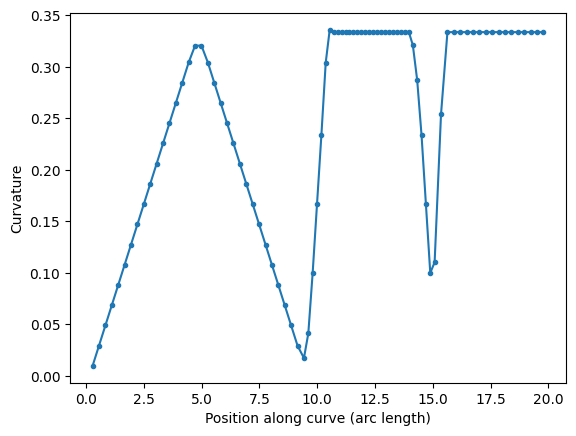

You can compare two 90 degrees euler bend with 180 euler bend.

A 180 euler bend is shorter, and has less loss than two 90 degrees euler bend.

straight_points = 100

P = gf.Path()
P.append(
    [
        gf.path.euler(radius=3, angle=90, p=1, use_eff=False),
        gf.path.euler(radius=3, angle=90, p=1, use_eff=False),
        gf.path.straight(length=6, npoints=100),
        gf.path.euler(radius=3, angle=180, p=1, use_eff=False),
    ]
)

f = P.plot()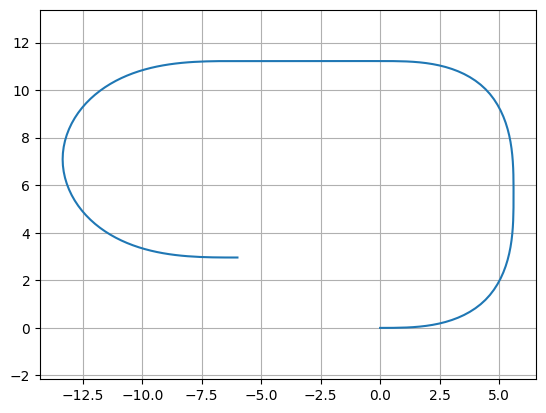

s, K = P.curvature()
plt.plot(s, K, ".-")
plt.xlabel("Position along curve (arc length)")
plt.ylabel("Curvature")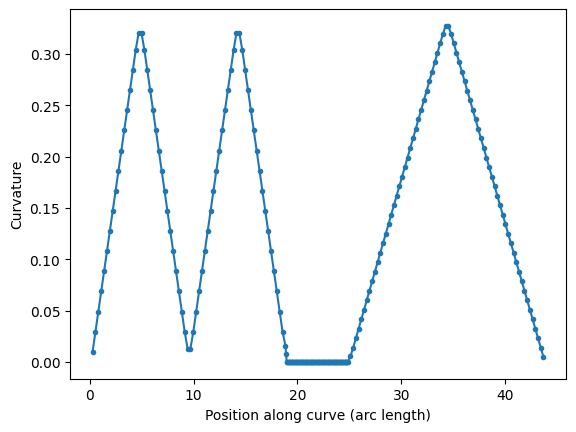

Transitioning between cross-sections¶

Often a critical element of building paths is being able to transition between cross-sections. You can use the transition() function to do exactly this: you simply feed it two CrossSections and it will output a new CrossSection that smoothly transitions between the two.

Let’s start off by creating two cross-sections we want to transition between. Note we give all the cross-sectional elements names by specifying the name argument in the add() function -- this is important because the transition function will try to match names between the two input cross-sections, and any names not present in both inputs will be skipped.

# Create our first CrossSection
import gdsfactory as gf

s0 = gf.Section(width=1.2, offset=0, layer=(2, 0), name="core", port_names=("o1", "o2"))
s1 = gf.Section(width=2.2, offset=0, layer=(3, 0), name="etch")
s2 = gf.Section(width=1.1, offset=3, layer=(1, 0), name="wg2")
X1 = gf.CrossSection(sections=[s0, s1, s2])

# Create the second CrossSection that we want to transition to
s0 = gf.Section(width=1, offset=0, layer=(2, 0), name="core", port_names=("o1", "o2"))
s1 = gf.Section(width=3.5, offset=0, layer=(3, 0), name="etch")
s2 = gf.Section(width=3, offset=5, layer=(1, 0), name="wg2")
X2 = gf.CrossSection(sections=[s0, s1, s2])

# To show the cross-sections, let's create two Paths and
# create Components by extruding them
P1 = gf.path.straight(length=5)
P2 = gf.path.straight(length=5)
wg1 = gf.path.extrude(P1, X1)
wg2 = gf.path.extrude(P2, X2)

# Place both cross-section Components and quickplot them
c = gf.Component()
wg1ref = c << wg1
wg2ref = c << wg2
wg2ref.movex(7.5)

c.plot()

Now let’s create the transitional CrossSection by calling transition() with these two CrossSections as input. If we want the width to vary as a smooth sinusoid between the sections, we can set width_type to 'sine' (alternatively we could also use 'linear').

# Create the transitional CrossSection
Xtrans = gf.path.transition(cross_section1=X1, cross_section2=X2, width_type="sine")

# Create a Path for the transitional CrossSection to follow
P3 = gf.path.straight(length=15, npoints=100)

# Use the transitional CrossSection to create a Component
straight_transition = gf.path.extrude_transition(P3, Xtrans)
straight_transition.plot()

Now that we have all of our components, let’s connect() everything and see what it looks like

c = gf.Component("transition_demo")

wg1ref = c << wg1
wgtref = c << straight_transition
wg2ref = c << wg2

wgtref.connect("o1", wg1ref.ports["o2"])
wg2ref.connect("o1", wgtref.ports["o2"])

c.plot()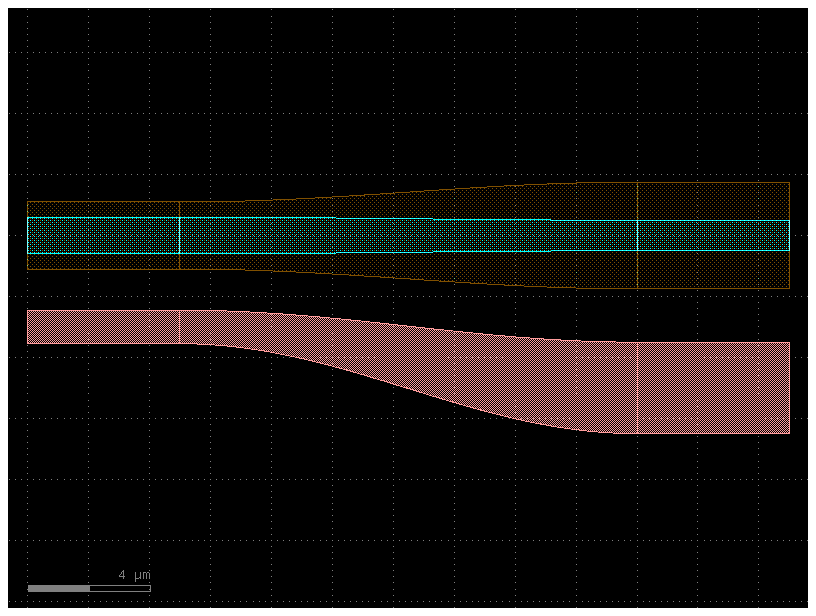

Note that since transition() outputs a Transition, we can make the transition follow an arbitrary path:

# Transition along a curving Path
P4 = gf.path.euler(radius=25, angle=45, p=0.5, use_eff=False)
wg_trans = gf.path.extrude_transition(P4, Xtrans)

c = gf.Component("demo_transition")
wg1_ref = c << wg1  # First cross-section Component
wg2_ref = c << wg2
wgt_ref = c << wg_trans

wgt_ref.connect("o1", wg1_ref.ports["o2"])
wg2_ref.connect("o1", wgt_ref.ports["o2"])

c.plot()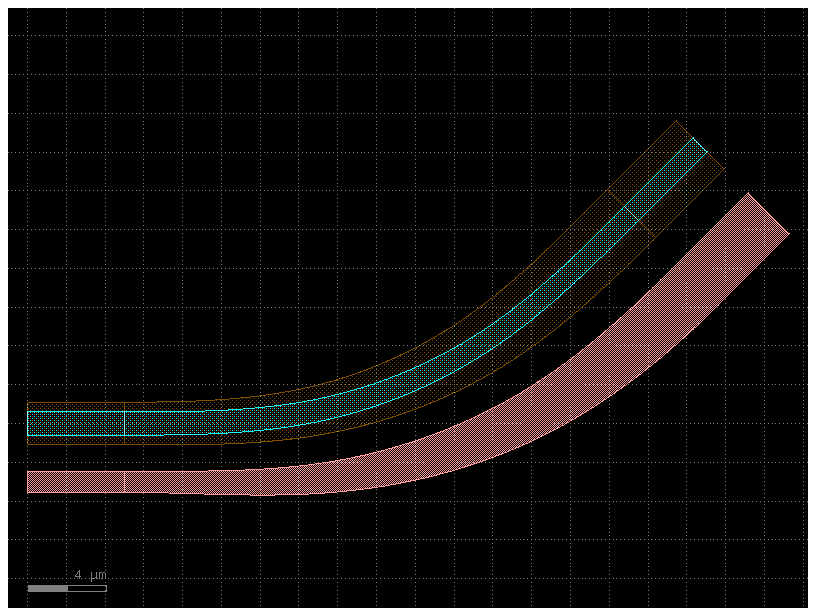

You can also extrude an arbitrary Transition:

w1 = 1
w2 = 5
x1 = gf.get_cross_section("strip", width=w1)
x2 = gf.get_cross_section("strip", width=w2)
transition = gf.path.transition(x1, x2)
p = gf.path.arc(radius=10)
c = gf.path.extrude_transition(p, transition)
c.plot()

Variable width / offset¶

In some instances, you may want to vary the width or offset of the path’s cross- section as it travels. This can be accomplished by giving the CrossSection arguments that are functions or lists. Let’s say we wanted a width that varies sinusoidally along the length of the Path. To do this, we need to make a width function that is parameterized from 0 to 1: for an example function my_width_fun(t) where the width at t==0 is the width at the beginning of the Path and the width at t==1 is the width at the end.

import numpy as np

import gdsfactory as gf


def my_custom_width_fun(t):
    # Note: Custom width/offset functions MUST be vectorizable--you must be able
    # to call them with an array input like my_custom_width_fun([0, 0.1, 0.2, 0.3, 0.4])
    num_periods = 5
    return 3 + np.cos(2 * np.pi * t * num_periods)


# Create the Path
P = gf.path.straight(length=40, npoints=30)

# Create two cross-sections: one fixed width, one modulated by my_custom_offset_fun
s0 = gf.Section(width=3, offset=-6, layer=(2, 0))
s1 = gf.Section(width=0, width_function=my_custom_width_fun, offset=0, layer=(1, 0))
X = gf.CrossSection(sections=(s0, s1))

# Extrude the Path to create the Component
c = gf.path.extrude(P, cross_section=X)
c.plot()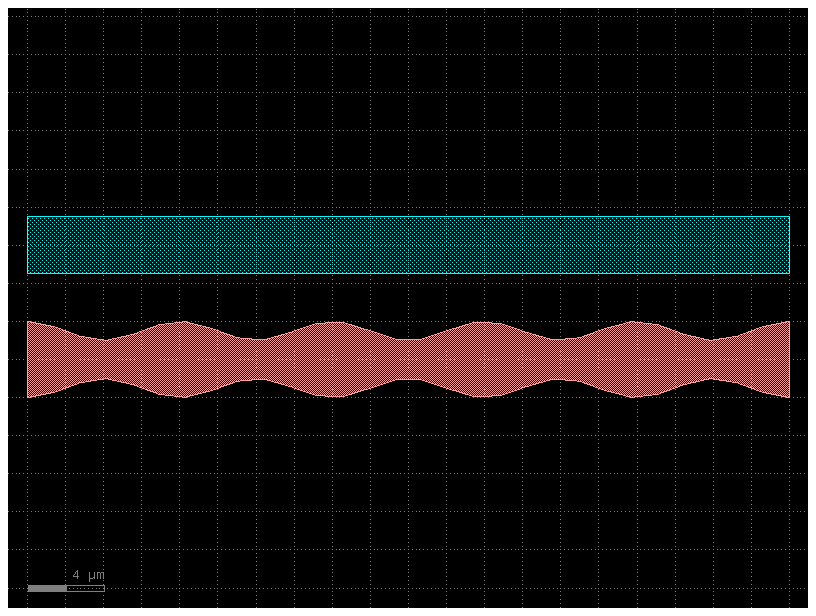

We can do the same thing with the offset argument:

def my_custom_offset_fun(t):
    # Note: Custom width/offset functions MUST be vectorizable--you must be able
    # to call them with an array input like my_custom_offset_fun([0, 0.1, 0.2, 0.3, 0.4])
    num_periods = 3
    return 3 + np.cos(2 * np.pi * t * num_periods)


# Create the Path
P = gf.path.straight(length=40, npoints=30)

# Create two cross-sections: one fixed offset, one modulated by my_custom_offset_fun
s0 = gf.Section(width=1, offset=0, layer=(1, 0))
s1 = gf.Section(
    width=1,
    offset_function=my_custom_offset_fun,
    layer=(2, 0),
    port_names=("clad1", "clad2"),
)
X = gf.CrossSection(sections=(s0, s1))

# Extrude the Path to create the Component
c = gf.path.extrude(P, cross_section=X)
c.plot()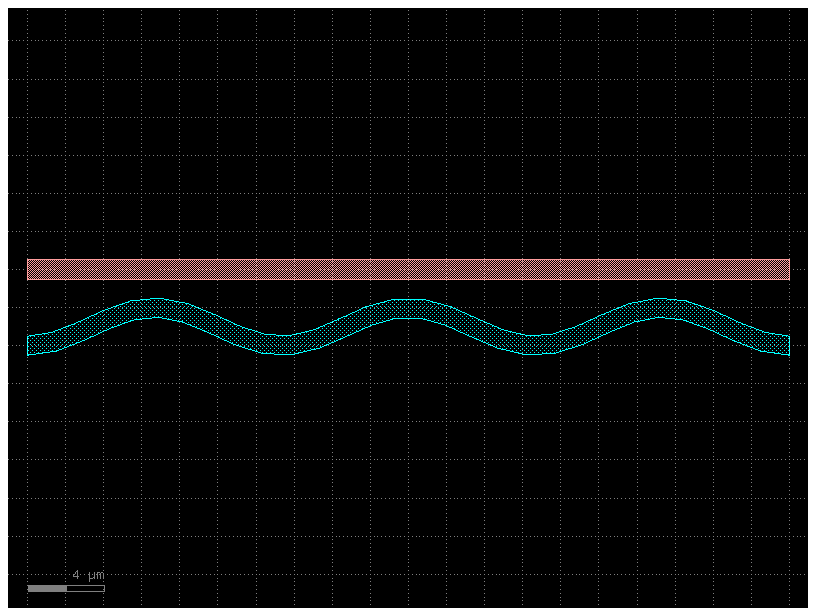

Offsetting a Path¶

Sometimes it’s convenient to start with a simple Path and offset the line it follows to suit your needs (without using a custom-offset CrossSection). Here, we start with two copies of simple straight Path and use the offset() function to directly modify each Path.

def my_custom_offset_fun(t):
    # Note: Custom width/offset functions MUST be vectorizable--you must be able
    # to call them with an array input like my_custom_offset_fun([0, 0.1, 0.2, 0.3, 0.4])
    num_periods = 3
    return 2 + np.cos(2 * np.pi * t * num_periods)


P1 = gf.path.straight(npoints=101)
P1.offset(offset=my_custom_offset_fun)
f = P1.plot()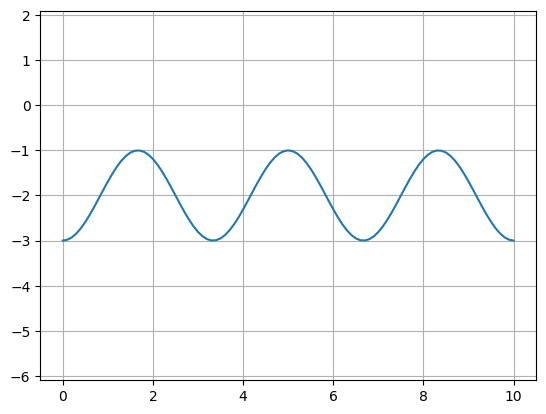

P2 = P1.copy()  # Make a copy of the Path
P2.mirror((1, 0))  # reflect across X-axis
f2 = P2.plot()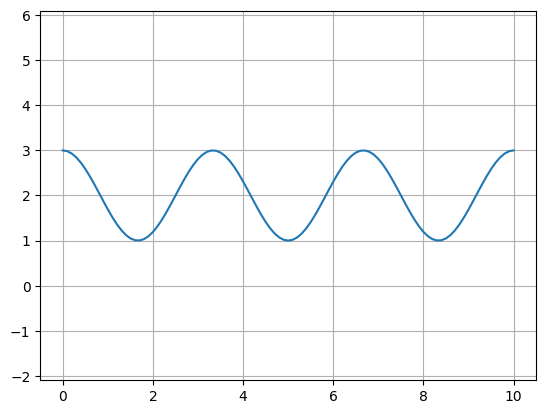

# Create the Path
P = gf.path.arc(radius=10, angle=45)

# Create two cross-sections: one fixed width, one modulated by my_custom_offset_fun
s0 = gf.Section(width=1, offset=3, layer=(2, 0), name="waveguide")
s1 = gf.Section(width=1, offset=0, layer=(1, 0), name="heater", port_names=("o1", "o2"))
X = gf.CrossSection(sections=(s0, s1))
c = gf.path.extrude(P, X)
c.plot()

P = gf.Path()
P.append(gf.path.arc(radius=10, angle=90))  # Circular arc
P.append(gf.path.straight(length=10))  # Straight section
P.append(gf.path.euler(radius=3, angle=-90))  # Euler bend (aka "racetrack" curve)
P.append(gf.path.straight(length=40))
P.append(gf.path.arc(radius=8, angle=-45))
P.append(gf.path.straight(length=10))
P.append(gf.path.arc(radius=8, angle=45))
P.append(gf.path.straight(length=10))

f = P.plot()

c = gf.path.extrude(P, width=1, layer=(2, 0))
c.plot()

s0 = gf.Section(width=2, offset=0, layer=(2, 0))
xs = gf.CrossSection(sections=(s0,))
c = gf.path.extrude(P, xs)
c.plot()

p = gf.path.straight(length=10, npoints=101)
s0 = gf.Section(width=1, offset=0, layer=(1, 0), port_names=("o1", "o2"), name="core")
s1 = gf.Section(width=3, offset=0, layer=(3, 0), name="slab")
x1 = gf.CrossSection(sections=(s0, s1))
c = gf.path.extrude(p, x1)
c.plot()

s0 = gf.Section(
    width=1 + 3, offset=0, layer=(1, 0), port_names=("o1", "o2"), name="core"
)
s1 = gf.Section(width=3 + 3, offset=0, layer=(3, 0), name="slab")
x2 = gf.CrossSection(sections=(s0, s1))
c2 = gf.path.extrude(p, x2)
c2.plot()

t = gf.path.transition(x1, x2)
c3 = gf.path.extrude_transition(p, t)
c3.plot()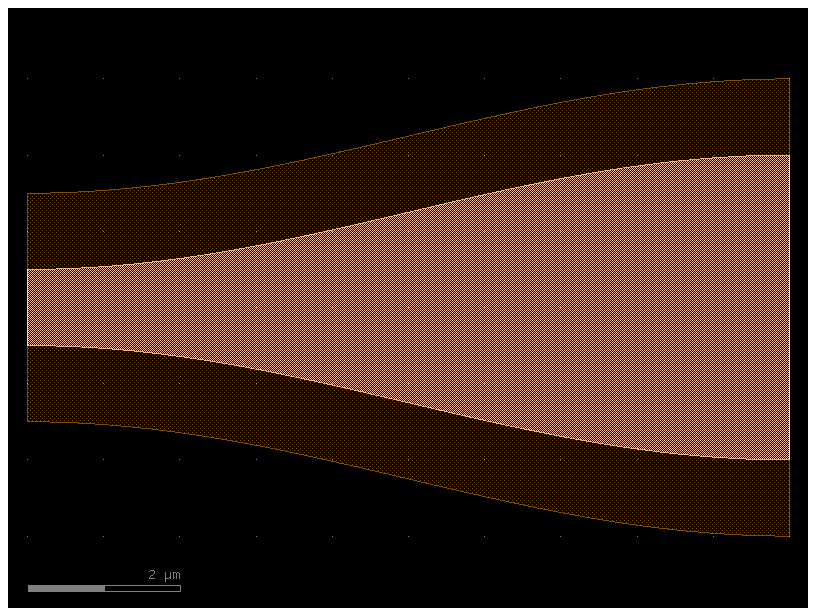

c4 = gf.Component()
start_ref = c4 << c
trans_ref = c4 << c3
end_ref = c4 << c2

trans_ref.connect("o1", start_ref.ports["o2"])
end_ref.connect("o1", trans_ref.ports["o2"])
c4.plot()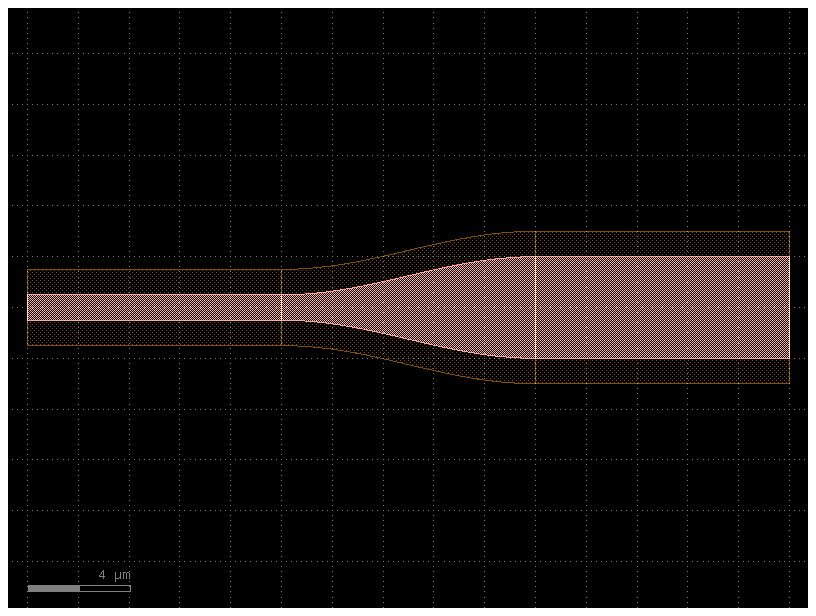

Creating new cross_sections¶

You can create functions that return a cross_section in 2 ways:

Customize an existing cross-section for example gf.cross_section.strip
Define a function that returns a cross_section
Define a CrossSection object

What parameters do cross_section take?

help(gf.cross_section.cross_section)

Help on function cross_section in module gdsfactory.cross_section:

cross_section(width: 'float' = 0.5, offset: 'float' = 0, layer: 'typings.LayerSpec' = 'WG', sections: 'Sections | None' = None, port_names: 'typings.IOPorts' = ('o1', 'o2'), port_types: 'typings.IOPorts' = ('optical', 'optical'), bbox_layers: 'typings.LayerSpecs | None' = None, bbox_offsets: 'typings.Floats | None' = None, cladding_layers: 'typings.LayerSpecs | None' = None, cladding_offsets: 'typings.Floats | None' = None, cladding_simplify: 'typings.Floats | None' = None, cladding_centers: 'typings.Floats | None' = None, radius: 'float | None' = 10.0, radius_min: 'float | None' = None, main_section_name: 'str' = '_default') -> 'CrossSection'
    Return CrossSection.
    
    Args:
        width: main Section width (um).
        offset: main Section center offset (um).
        layer: main section layer.
        sections: list of Sections(width, offset, layer, ports).
        port_names: for input and output ('o1', 'o2').
        port_types: for input and output: electrical, optical, vertical_te ...
        bbox_layers: list of layers bounding boxes to extrude.
        bbox_offsets: list of offset from bounding box edge.
        cladding_layers: list of layers to extrude.
        cladding_offsets: list of offset from main Section edge.
        cladding_simplify: Optional Tolerance value for the simplification algorithm.                 All points that can be removed without changing the resulting.                 polygon by more than the value listed here will be removed.
        cladding_centers: center offset for each cladding layer. Defaults to 0.
        radius: routing bend radius (um).
        radius_min: min acceptable bend radius.
        main_section_name: name of the main section. Defaults to _default
    
    .. plot::
        :include-source:
    
        import gdsfactory as gf
    
        xs = gf.cross_section.cross_section(width=0.5, offset=0, layer='WG')
        p = gf.path.arc(radius=10, angle=45)
        c = p.extrude(xs)
        c.plot()
    
    .. code::
    
    
           ┌────────────────────────────────────────────────────────────┐
           │                                                            │
           │                                                            │
           │                   boox_layer                               │
           │                                                            │
           │         ┌──────────────────────────────────────┐           │
           │         │                            ▲         │bbox_offset│
           │         │                            │         ├──────────►│
           │         │           cladding_offset  │         │           │
           │         │                            │         │           │
           │         ├─────────────────────────▲──┴─────────┤           │
           │         │                         │            │           │
        ─ ─┤         │           core   width  │            │           ├─ ─ center
           │         │                         │            │           │
           │         ├─────────────────────────▼────────────┤           │
           │         │                                      │           │
           │         │                                      │           │
           │         │                                      │           │
           │         │                                      │           │
           │         └──────────────────────────────────────┘           │
           │                                                            │
           │                                                            │
           │                                                            │
           └────────────────────────────────────────────────────────────┘

import gdsfactory as gf
from gdsfactory.cross_section import CrossSection, cross_section, xsection
from gdsfactory.typings import LayerSpec

@xsection
def pin(
    width: float = 0.5,
    layer: LayerSpec = "WG",
    radius: float = 10.0,
    radius_min: float = 5,
    layer_p: LayerSpec = (21, 0),
    layer_n: LayerSpec = (20, 0),
    width_p: float = 2,
    width_n: float = 2,
    offset_p: float = 1,
    offset_n: float = -1,
    **kwargs,
) -> CrossSection:
    """Return PIN cross_section."""
    sections = (
        gf.Section(layer=layer_p, width=width_p, offset=offset_p),
        gf.Section(layer=layer_n, width=width_n, offset=offset_n),
    )

    return cross_section(
        width=width,
        layer=layer,
        radius=radius,
        radius_min=radius_min,
        sections=sections,
        **kwargs,
    )

c = gf.components.straight(cross_section=pin)
c.plot()

pin5 = gf.components.straight(cross_section=pin, length=5)
pin5.plot()

pin5 = gf.components.straight(cross_section="pin", length=5)
pin5.plot()

finally, you can also pass most components Dict that define the cross-section

# Create our first CrossSection
s0 = gf.Section(width=0.5, offset=0, layer=(1, 0), name="wg", port_names=("o1", "o2"))
s1 = gf.Section(width=0.2, offset=0, layer=(3, 0), name="slab")
x1 = gf.CrossSection(sections=(s0, s1))

# Create the second CrossSection that we want to transition to
s0 = gf.Section(width=0.5, offset=0, layer=(1, 0), name="wg", port_names=("o1", "o2"))
s1 = gf.Section(width=3.0, offset=0, layer=(3, 0), name="slab")
x2 = gf.CrossSection(sections=(s0, s1))

# To show the cross-sections, let's create two Paths and create Components by extruding them
p1 = gf.path.straight(length=5)
p2 = gf.path.straight(length=5)
wg1 = gf.path.extrude(p1, x1)
wg2 = gf.path.extrude(p2, x2)

# Place both cross-section Components and quickplot them
c = gf.Component()
wg1ref = c << wg1
wg2ref = c << wg2
wg2ref.movex(7.5)

# Create the transitional CrossSection
xtrans = gf.path.transition(cross_section1=x1, cross_section2=x2, width_type="linear")
# Create a Path for the transitional CrossSection to follow
p3 = gf.path.straight(length=15, npoints=100)

# Use the transitional CrossSection to create a Component
straight_transition = gf.path.extrude_transition(p3, xtrans)
straight_transition.plot()

# Create the transitional CrossSection
xtrans = gf.path.transition(
    cross_section1=x1, cross_section2=x2, width_type="parabolic"
)
# Create a Path for the transitional CrossSection to follow
p3 = gf.path.straight(length=15, npoints=100)

# Use the transitional CrossSection to create a Component
straight_transition = gf.path.extrude_transition(p3, xtrans)
straight_transition.plot()

# Create the transitional CrossSection
xtrans = gf.path.transition(cross_section1=x1, cross_section2=x2, width_type="sine")
# Create a Path for the transitional CrossSection to follow
p3 = gf.path.straight(length=15, npoints=100)

# Use the transitional CrossSection to create a Component
straight_transition = gf.path.extrude_transition(p3, xtrans)
straight_transition.plot()

s = straight_transition.to_3d()
s.show()

The port location, width and orientation remains the same for a sheared component. However, an additional property, shear_angle is set to the value of the shear angle. In general, shear ports can be safely connected together.

bbox_layers vs cladding_layers¶

For extruding waveguides you have two options:

bbox_layers for squared bounding box
cladding_layers for extruding a layer that follows the shape of the path.

xs_bbox = gf.cross_section.cross_section(bbox_layers=((3, 0),), bbox_offsets=(3,))
w1 = gf.components.bend_euler(cross_section=xs_bbox)
w1.plot()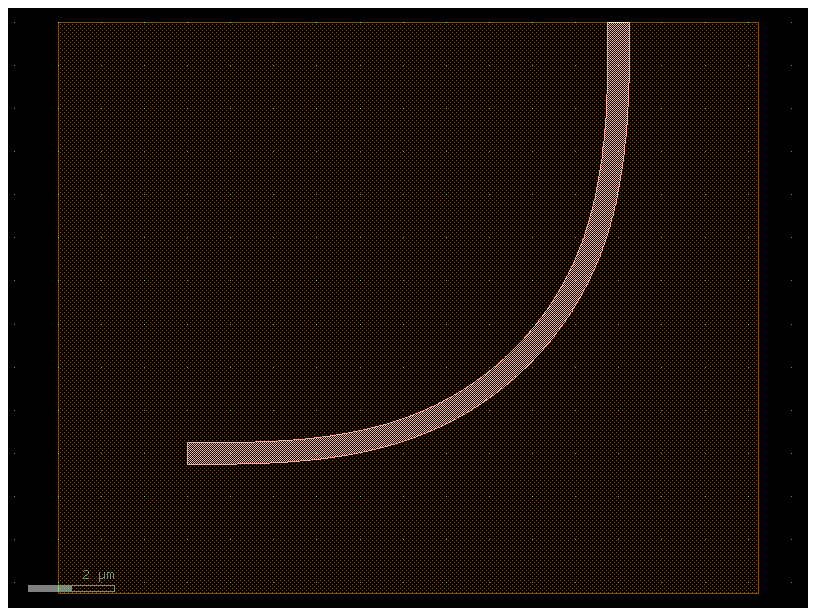

xs_clad = gf.cross_section.cross_section(cladding_layers=[(3, 0)], cladding_offsets=[3])
w2 = gf.components.bend_euler(cross_section=xs_clad)
w2.plot()

Insets¶

It’s handy to be able to extrude a CrossSection along a Path, while each Section may have a particular inset relative to the main Section. An example of this is a waveguide with a heater.

import gdsfactory as gf


@xsection
def xs_waveguide_heater() -> gf.CrossSection:
    return gf.cross_section.cross_section(
        layer="WG",
        width=0.5,
        sections=(
            gf.cross_section.Section(
                name="heater",
                width=1,
                layer="HEATER",
                insets=(1, 2),
            ),
        ),
    )


c = gf.components.straight(cross_section=xs_waveguide_heater)
c.plot()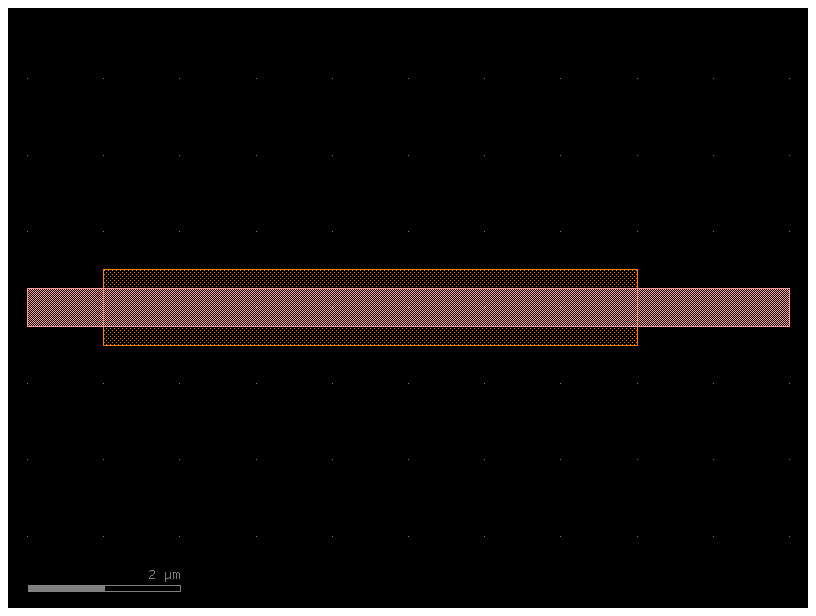

@xsection
def xs_waveguide_heater_with_ports() -> gf.CrossSection:
    return gf.cross_section.cross_section(
        layer="WG",
        width=0.5,
        sections=(
            gf.cross_section.Section(
                name="heater",
                width=1,
                layer="HEATER",
                insets=(1, 2),
                port_names=("e1", "e2"),
                port_types=("electrical", "electrical"),
            ),
        ),
    )


c = gf.components.straight(cross_section=xs_waveguide_heater_with_ports)
c.plot()